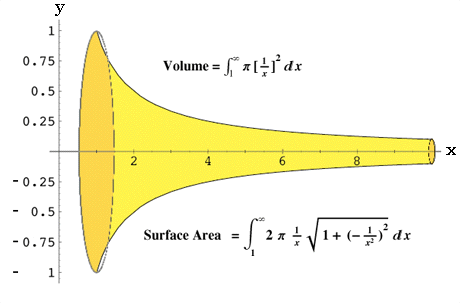
Above is a representation of the graph of the equation y = 1/x as it would look
if it were rotated about the x axis. In Calculus you learn that the volume of
this object (if x was allowed to increase to infinity) is finite. That is, if
you were to continually pour a liquid into it, it would eventually overflow.
However, the surface area is infinite. You could never cover the entire surface
with paint. The thing that struck me about this was how much the graph resembled
the bell of a trumpet. I guess others have noticed this also, because this graph
is known as "Gabriel's Horn". I wonder if the above facts explain why you can
make a trumpet sound beautiful, but you can never keep it looking that way.

<<< Back to home